An interesting question is what kind of correlation matrices are possible with three variables (A, B and C). If we know, that there is a correlation between A and B as well as B and C, what kind of correlation can occur between A and C. What are the possible maximum values of the correlation between A and B and between B and C, when the correlation between A and C variables is null?
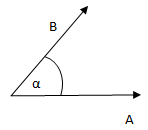
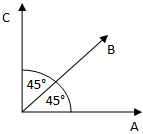
The correlation can be interpreted as the cosine of the angle between the normalized vectors of the variables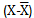 
.
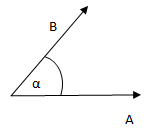
cor(A,B) = cos(α)
Therefore the correlation between A and C is null, if their vectors are orthogonal (cos (90°)=0). The correlation between the variables is higher, if the angle between their vectors is smaller, so if the angle between A and C vectors is fixed, the correlation between A and B as well as between B and C variables is the largest, if the vector of the B variable is in the same plane like the vectors of A and C variables.
For example, if the correlation between A and B, B and C variables are the same, then its maximum value is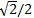 
(cos(45°)), when the correlation between A and C is null.
Let’s see how it works in practice!
We are generating 3 normally distributed random variables (n = 1000).
> options(digits=7)
> set.seed(234)
>
> M <- matrix(rnorm(3000), ncol=3)
> colnames(M) <- c(“A”, “B”, “C”)
> head(M)
A B C
[1,] -1.34352141 -0.158314852 -0.41120490
[2,] 0.62177555 0.018813945 -0.27796435
[3,] 0.80087466 0.498246468 0.40257018
[4,] -1.38889241 -1.675263002 0.45676675
[5,] -0.71435686 3.003174741 -0.43762865
[6,] -0.32406105 -0.608898653 1.36512746
We are defining the desired correlation matrix. The value of the variable maxCor is 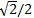(rounded down), i.e., the maximal correlation between A and B, B and C variables, if they are the same values and the correlation between A and C variables is 0.
> maxCor <- floor(1e7*sqrt(2)/2)/1e7
> CM <- matrix(c(1,maxCor,0,
+ maxCor,1,maxCor,
+ 0,maxCor,1), nrow=3)
> colnames(CM) <- c(“A”, “B”, “C”)
> rownames(CM) <- c(“A”, “B”, “C”)
> CM
A B C
A 1.0000000 0.7071067 0.0000000
B 0.7071067 1.0000000 0.7071067
C 0.0000000 0.7071067 1.0000000
We change the values of the 3 generated variables in order to reach the given correlation matrix with Cholesky decomposition.
> L <- chol(CM)
> ABC <- ABC %*% t(L)
> head(ABC)
A B C
[1,] -1.45546690 -0.52315033 -0.00027866842
[2,] 0.63507902 -0.26466082 -0.00018837296
[3,] 1.15318808 0.75488359 0.00027281678
[4,] -2.57348211 -0.72782332 0.00030954511
[5,] 1.40920812 1.68593692 -0.00029657546
[6,] -0.75461737 0.93457073 0.00092512980
Let’s see if the correlations between the variable are as we wanted!
> cor(ABC)
A B C
A 1.000000000 0.35850510 0.034449684
B 0.358505099 1.00000000 0.812815583
C 0.034449684 0.81281558 1.000000000
The correlation matrix is not the most successful, however, as we can see a distribution like this is theoretically possible.
What happens if we increase a little the correlation between A and B, B and C variables (with 0.0000001)?
> maxCor <- floor(1e7*sqrt(2)/2)/1e7+1e-7
> CM <- matrix(c(1,maxCor,0,
+ maxCor,1,maxCor,
+ 0,maxCor,1), nrow=3)
> L <- chol(CM)
Error in chol.default(CM) :
the leading minor of order 3 is not positive definite
We get an error message, because such distribution doesn’t exist. The desired correlation matrix is not positive definite, there is a negative eigenvalue, so it can not be a correlation matrix. If the correlation between A and B, B and C variables are greater than , then the correlations between A and C cannot be 0.
> eigen(CM)
$values
[1] 2.0000000e+00 1.0000000e+00 -2.6606238e-08$vectors
[,1] [,2] [,3]
[1,] 0.50000000 -7.0710678e-01 0.50000000
[2,] 0.70710678 -4.4408920e-16 -0.70710678
[3,] 0.50000000 7.0710678e-01 0.50000000
Of course the correlation between A and B, B and C variables can be less than these values, because if the vector of the B variable is not in the plane of the vectors of A and C variables, then the angles between A and B, B and C variables can be larger, so the correlations between them are smaller.
Similarly, if the correlations between A and B, B and C are different, for example the angle between the vectors of the A and B variables is 55°, the correlation between the B and C is maximal if the angle between the corresponding vectors is 90° – 55° = 35°. So, if the correlation between A and B is cos(55°) = 0.574, the correlation between A and C can be 0, if the correlation between the variables B and C is maximum cos (35°) = 0.819.
> maxCorAB <- 0.5735764
> maxCorBC <- 0.8191520
> CM <- matrix(c(1,maxCorAB,0,
+ maxCorAB,1,maxCorBC,
+ 0,maxCorBC,1), nrow=3)
> CM
[,1] [,2] [,3]
[1,] 1.0000000 0.5735764 0.000000
[2,] 0.5735764 1.0000000 0.819152
[3,] 0.0000000 0.8191520 1.000000
>
> L <- chol(CM)
>
> ABC <- M %*% t(L)
>
> cor(ABC)
[,1] [,2] [,3]
[1,] 1.000000000 0.3341330 0.032695729
[2,] 0.334132999 1.0000000 0.770568600
[3,] 0.032695729 0.7705686 1.000000000
If, however, we increase slightly the correlation between the A and B or B and C variables than the maximum value, we get an error message again.
> maxCorAB <- 0.5735764+1e-7
> maxCorBC <- 0.8191520
> CM <- matrix(c(1,maxCorAB,0,
+ maxCorAB,1,maxCorBC,
+ 0,maxCorBC,1), nrow=3)
>
> L <- chol(CM)
Error in chol.default(CM) :
the leading minor of order 3 is not positive definite
>
> maxCorAB <- 0.5735764
> maxCorBC <- 0.8191520+1e-7
> CM <- matrix(c(1,maxCorAB,0,
+ maxCorAB,1,maxCorBC,
+ 0,maxCorBC,1), nrow=3)
>
> L <- chol(CM)
Error in chol.default(CM) :
the leading minor of order 3 is not positive definite
The correlations between the variables are not independent. Correlation between two variables is possible only within a given framework (even if this framework is quite wide), if the correlation between them and a third variable is given.
RManic 